Label, Domain and Tasks: A Definition

Here is a brief definition of label, domain and the tasks (Yang et al. 2020).

A domain $\mathbb{D}$ consists of:

• a feature space $\mathscr{X}$ and
• a marginal probability distribution $\mathbb{P}^X$, where each input instance $x \in \mathscr{X}$.

Two domains are different when they have different feature space or different marginal probability distributions. Given a specific domain $\mathbb{D} = \{\mathscr{X}, \mathbb{P}^X\}$, a task, $\mathbb{T}$ consists of two components:

• a label space $\mathscr{Y}$ and
• a function $f(\cdot)$.

Therefore, $\mathbb{T} = \{\mathscr{Y}, f(\cdot)\}$. The function $f(\cdot)$ is a predictive function that can be used to make prediction on unseen instances, $\{x^*\}$.

From a probabilistic perspective $f(\cdot)$ can be written as $P(y|x)$ where $y \in \mathscr{Y}$. Given a source domain $\mathbb{D}_s$ and a target domain $\mathbb{D}_t$ the condition $\mathbb{D}_s \neq \mathbb{D}_t$ implies that either $\mathscr{X}_s \neq \mathscr{X}_t$ or $\mathbb{P}^{X_s} \neq \mathbb{P}^{X_t}$. Similarly, given source task $\mathbb{T}_s$ and target task $\mathbb{T}_t$, the condition $\mathbb{T}_s \neq \mathbb{T}_t$ implies that either $\mathscr{Y}_s \neq \mathscr{Y}_t$ or $\mathbb{P}^{Y_s|X_s} \neq \mathbb{P}^{Y_t|X_t}$.

Domain Adaptation and Transfer Learning

When the target domain and the source domain are the same,that is, $\mathbb{D}_s = \mathbb{D}_t$, and their learning tasks are the same, that is, $\mathbb{T}_s = \mathbb{T}_t$, the learning problem becomes a traditional machine learning problem.

Given such scenario, the objective of transfer learning algorithm is to improve the learning of the target predictive function $f(\cdot)$ for $\mathbb{D}_t$ using the knowledge in $\mathbb{D}_s$ and $\mathbb{T}_s$. If there is some overlap in the feature space between the domains and the label space are identical (i.e. $\mathscr{X}_s \cap \mathscr{X}_t \neq \varnothing$ and $\mathscr{Y}_s = \mathscr{Y}_t$), but the marginal or the conditional probability distributions are dissimilar ($\mathbb{P}^{X_s} \neq \mathbb{P}^{X_t}$ or $\mathbb{P}^{Y_s|X_s} \neq \mathbb{P}^{Y_t|X_t}$), the problem is categorized as homogeneous transfer. On the other hand, if there is no overlap between the feature spaces or the label spaces are not of similar (i.e. $\mathscr{X}_s \cap \mathscr{X}_t = \varnothing$ or $\mathscr{Y}_s \neq \mathscr{Y}_t$), the problem is categorized as heterogeneous transfer. As we can see, these inter-domain and inter-task discrepancies can give us a number of scenarios:

• The domains are similar but the tasks are different ($\mathbb{D}_s = \mathbb{D}_t$ but $\mathbb{T}_s \neq \mathbb{T}_t$), for example, when we have ADL data from a few persons on 4 activities, but asked to classify samples of the same persons’ containing a new activity previously unseen during training. This falls under inductive transfer learning (Redko et al. 2020).
• The tasks are similar but domains are different ($\mathbb{D}_s \neq \mathbb{D}_t$ but $\mathbb{T}_s = \mathbb{T}_t$), one example of this case is the classical transfer learning scenario where we want transfer persons, devices, body positions etc, assuming that the label space remains same. This is more specifically called transductive transfer learning or domain adaptation.
• Both domains and the tasks are related but dissimilar ($\mathbb{D}_s \neq \mathbb{D}_t$ and $\mathbb{T}_s \neq \mathbb{T}_t$); this is one of the most challenging scenarios and have not been greatly been explored in the literature. This is called purely unsupervised transfer learning.

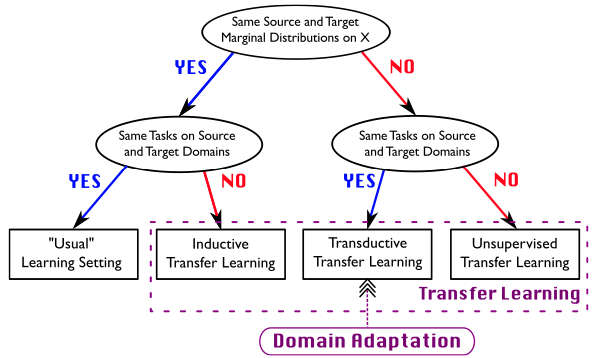
Figure 1: Comparison of standard supervised learning, transfer learning, and positioning of the domain adaptation. (Redko et al. 2020)